Open Question #1

Why could these shapes be sorted together? What other shapes would go with them?
If these two shapes were sorted into two different groups, what could the groups be for? What other shapes would go with each shape?

Sample answer:
I could sort by colour so that they go together. All the blue shapes could go together, so I could add triangles, rectangles, and circles that are also blue. The shapes of other colours would not go with these ones.
These shapes would not be in the same group if I sorted by the number of sides. I could have four-sided shapes and not four-sided shapes. The squares and rectangles would go together, and the hexagons and triangles would go together.

Open Question #2

What numbers might be missing in this pattern?
___, 7, 10, ___, ___, ___, 10, ___, 4, ___, 10, ___

Sample answers:
4, 7, 10, 7, 4, 7, 10, 7, 4, 7, 10, 7
OR
4, 7, 10, 10, 4, 7, 10, 10, 4, 7, 10, 10

 

Open Question #3

The answer to a question could be either “square” or “rectangle.” What might the question be? Sample answers: What shape other than a triangle do you see on a triangle-based prism? OR What quadrilateral has four right angles? OR What 2-D shape do you see on a cube?

Open Question #4

A shrinking pattern includes the numbers 200, 120, and 40. What might the pattern be? Sample answers: 200, 180, 160, 140, 120, 100, 80, 60, 40, … OR 300, 280, 260, 240, 220, 200, 180, 160, 140, 120, 100, 80, 60, 40, …

Open Question #5

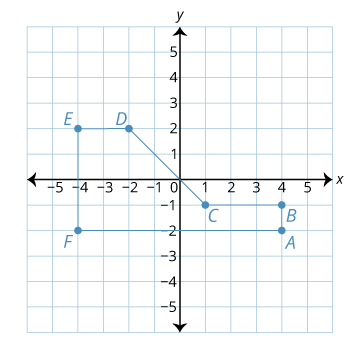
Draw a polygon on a Cartesian coordinate grid with these conditions:
• It has at least one vertex in each of three of the four quadrants.
• It has one or more right angles.
• It has at least one set of parallel sides.
Give a classmate the coordinates for one vertex of your polygon. Call this vertex A. Then, give instructions on how to get to the next vertex, B, without saying its coordinates. Continue giving your classmate directions until they have plotted all of the vertices of your polygon. Finally, tell them how to connect the vertices to make your polygon.

Sample answer:
• Plot point A at (4, –2).
• Go up 1 unit to plot point B.
• Go left 3 units to plot point C.
• Go up 3 units and left 3 units to plot point D.
• Go left 2 units to plot point E.
• Go down 4 units to plot point F.
• Connect the points in alphabetical order. Then connect F to A.

Open Question #6

Draw a graph of a linear growing pattern that goes through (6, –8). What is the general term for your graph? Show two solutions.

Sample answer: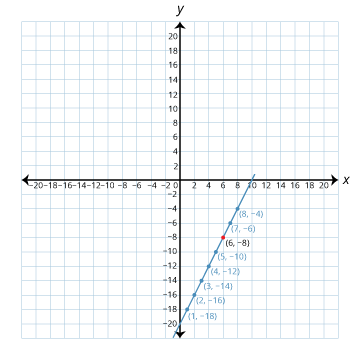

The general term is 2n – 20.

The general term is 52 – 10n.