Block Builder

What You’ll Need: Red pattern blocks What shapes can you make using exactly 6 red pattern blocks? They have to touch to make one whole shape. Sample answer: I made shapes with 14 sides but also a shape with 6 sides.

Square Sequences

What You’ll Need:
A variety of shapes in a variety of colours

Create a pattern where the third shape and the eighth shape are squares.

Sample answer:
I made these patterns:

Ten-Frame Fascination

What You’ll Need:
Ten-Frame Fascination printout
Counters

Print and cut out the 10-frames from the Ten-Frame Fascination printout. Provide students with the 10-frames and counters. Then give students these instructions:
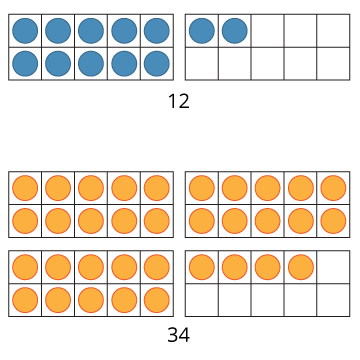
What numbers can you represent where the number of counters in the last unfilled 10-frame is one more than the number of full 10-frames? What do you notice about the numbers?

Sample answer:
I notice that the ones amount is always one more than the tens amount.

High or Low

What You’ll Need:
High or Low printout

Print and cut out the number cards from the High or Low printout. Shuffle the cards and place them face down in a pile. Then give students these instructions:
Play with a partner or in a small group. Each player picks up two cards without showing them to the other players. Each player adds their cards together. If the sum of their cards is 4 or 14, they get 2 points. If the sum of their cards is 5 or 15, they get 1 point. The first player with 10 points wins.

Example:
Codey picked 7 and 1. He adds them together to get 8. Codey does not get any points.
Melanie picked up 9 and 6. She adds them together to get 15. Melanie gets 1 point because the sum of her cards is 15.
Henry picked up a 1 and 3. He adds them together to get 4. Henry gets 2 points because his numbers equal 4.

Consecutive Count

What You’ll Need: No materials necessary What numbers are you able to write as the sum of consecutive numbers (i.e., numbers that are “in a row” numbers). You can use any number of consecutive numbers. Are there any numbers you cannot write that way? Answer: 1 = 0 + 1 2 cannot be written that way. 3 = 1 + 2 4 cannot be written that way. 5 = 2 + 3 6 = 1 + 2 + 3 7 = 3 + 4 8 cannot be written that way. 9 = 4 + 5 10 = 1 + 2 + 3 + 4 I can see that any odd number works, but only some even numbers do.

Square Seventeen

What You’ll Need: No materials necessary Square numbers are numbers such as 3 × 3 or 8 × 8, where the two numbers multiplied are the same. How can you arrange the numbers from 1 to 17 in a row so that each pair of numbers next to each other adds to a square number? Sample answer: 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17

First to Five

What You’ll Need: First to Five printout Print and cut out the number cards from the First to Five printout. Shuffle and place the cards face down in a pile. Then give students these instructions: Play in pairs or in a small group. Each player picks up six cards without showing them to the other players. Each player creates two decimals in this form: ☐.☐☐. The player whose number is closest to 5 when their two decimals are added together gets 1 point. The first player with 10 points wins. Example: Taylor picked up 7, 5, 1, 3, 2, and 8. She creates the numbers 3.28 and 1.75 because 3.28 is close to 3.25 and 3.25 + 1.75 equals 5. When her decimals are added together, her number is 5.03. Roger picked up 9, 6, 2, 1, 5, and 4. He creates the numbers 2.95 and 1.64 because 2.95 is close to 3 and 1.64 is close to 2 and 3 + 2 equals 5. When his decimals are added together, his number is 4.59. Taylor gets 1 point because her number is closer to 5.

Grid Guide

What You’ll Need:
Grid Guides printout

Print and cut out the grid from the Grid Guide printout. Then give students these instructions:
Colour two squares on your grid. Create a set of exactly five instructions, including instructions about moving up or down a certain number of spaces, left or right a certain number of spaces, or quarter or half turns either clockwise or counterclockwise that will get you from one of the coloured squares to the other.

Sample answer:

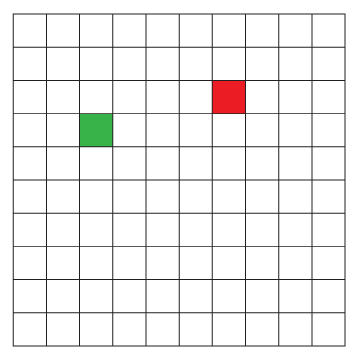
Go up 1 space.
Go right 3 spaces.
Go down 1 space.
Go right 1 space.
Go up 1 space.

Tearing Triangles printout

What You’ll Need:
Tearing Triangles printout

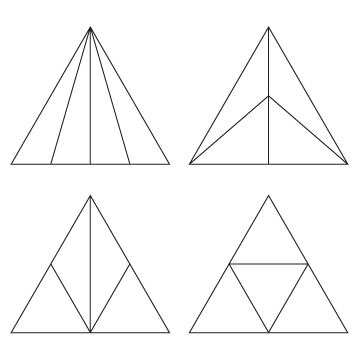
What are some different ways to cut an equilateral triangle into four triangles of equal area?

Sample answer:

Statistic Seekers

What You’ll Need: Statistic Seekers printout Pencil Print the blank chart from the Statistic Seekers printout. Provide each student with a chart. Then give students these instructions: Fill in the chart to make the descriptions of the rows and columns true. Sample answers: Sample answers can be found in the Statistic Seekers printout.

Concentration: Fractions and Percents II

What You’ll Need: Concentration: Fractions and Percents II printout Paper and pencil Print and cut out the concentration cards from the Concentration: Fractions and Percents II printout. Shuffle and place the concentration cards face down in a 6 × 5 array. Then give students these instructions: Play with a partner. Take turns flipping over two cards at a time. If the cards are a percent and a matching equivalent fraction, pick up those cards and take another turn. If they do not match, place them back in their original position and end your turn. Use paper and a pencil for fractions that are difficult to calculate. Play until all the cards have been matched. The player with the most matches wins.

Team-Up Timing

What You’ll Need:
No materials necessary

Connor can finish a job in 10 hours, but it would take Noah 8 hours.
How long would it take them if they worked together?

Sample answer:
I figured out that in 1 hour, Connor does (frac{1}{10}) of the job and Noah does (frac{1}{8}) of the job. This means that in one hour, Connor and Noah complete (frac{1}{10}) + (frac{1}{8}) of the job. That is (frac{9}{40}) of the job. That means that in 4 hours, they would do (frac{36}{40}) of the job, or (frac{9}{10}) of the job.
For the other tenth, it would take (frac{1}{9}) of 4 hours. Since 4 hours is 240 minutes, then (frac{1}{9}) of that time is 26(frac{2}{3}) minutes, so the total amount of time is a little less than 4(frac{1}{2}) hours, about 3(frac{1}{3}) minutes less.