Ask Marian
Can you suggest playground games that reinforce math understanding for younger children?
You might create a giant number line and have kids perform moves on the number line; for example, have them stand on 5 and move 3 steps forward. You might set up a more elaborate number-line scenario where one student gives instructions to another and the first to land on a mystery number wins the game.
Or you might play a game, such as Battleship or a treasure hunt, on a large coordinate grid that you could make using chalk or masking tape.
I’ve seen a game called “place-value toss,” where disposable pie plates are labelled, for example, “hundreds,” ”tens,” and “ones.” Each child tosses the same number of small objects toward the plates and makes a number based on where the objects land. For example, if a child tosses some beanbags and 2 land in the ones plate, 3 in the tens plate, and 5 in the hundreds plate, their number would be 532. The child with the greatest number wins.
I’ve also seen a game played on a hopscotch grid, where players hop on one foot for odd numbers and two feet for even numbers. The first person to hop through all the numbers without making a mistake wins.
What is the best way to show a student why a pattern that goes up by 3 uses a 3n in its pattern rule?
One way that has worked for me is to create a table of values that relates any pattern that goes up by 3 to the 3 times table.
It might look like this for the pattern 5, 8, 11, 14, … :
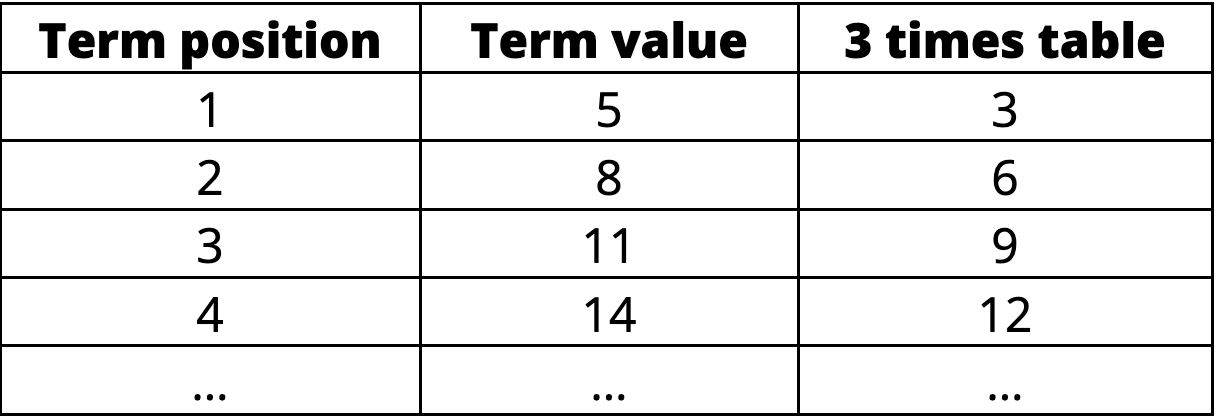
When students look at this table of values, they will realize that the value in the 3 times table column is always 3 × the term position.
But they will also see that the term value is always 2 more than the 3 times table number. So, the rule for the pattern would have to be 3n + 2.
I like using 100-charts with my students. What are some good questions I could ask using 100-charts?
- A number is in the bottom half of a 100-chart. What do you know for sure about that number?
- A number is directly below the number 26 in a 100-chart. What do you know for sure about that number?
- In a 100-chart, colour all the numbers that add to 10 when you add the ones digit to the tens digit. What sort of pattern do you see? Why does that pattern happen?
- What moves do you make in a 100-chart to add 12 to a number?
- Colour all the multiples of 4 in a 100-chart. How many numbers are coloured in each row? Why are there that many?
- Colour all the multiples of 9 in a 100-chart. Why do they make the pattern they do?
- Form a 2-by-2 square somewhere in a 100-chart. Add the numbers on each diagonal. What do you notice? Why does that happen?