Shareables
Grades K–2

Far Flyer
What You’ll Need: Paper
Vegetable Variety
What You’ll Need: No materials necessary Have students describe what vegetables they would use if they were making vegetable soup. Let them decide how many of each vegetable or how many pieces of each vegetable they would put in the soup. Then have them figure out how many vegetable pieces they used altogether. Sample answer: I decided my vegetable soup would have 3 carrots, 2 potatoes, and 1 celery stick. There are 6 vegetables in my soup. If I cut the carrots into 3 pieces and the potatoes into 2 pieces and the celery stick into 4 pieces, I would have a total of 17 vegetable pieces.
Star Subtraction
What You’ll Need:Star Subtraction printout
Print and cut out the number cards from the Star Subtraction printout. Then give students these instructions:
Play in pairs with the cards in a pile. Each player picks up 3 cards without revealing them to the other player. Players form a one-digit and two-digit number and subtract the one-digit number from the two-digit number. If their answer is less than 10, the player gets 2 points. If their answer is between 10 and 20, the player gets 1 point. If the answer is above 20, the player does not get any points. Mix the cards back into the pile of cards for the next round. The first player with 10 points wins.
Example:
David picks up 4, 2, and 6. He decides to make the equation 24 – 6 = 18. David gets 1 point.
Walter picks up 7, 5, and 1. He decides to make the equation 15 – 7 = 8. Walter gets 2 points.

Rectangle Rebuilding
What You’ll Need:Rectangle Rebuilding printout
Scissors
Ask students to cut a rectangle into a given number of shapes. For example, students could be asked to cut the rectangle into 3 smaller rectangles and 2 triangles, 2 squares and 2 triangles, or 2 smaller rectangles and 4 triangles.
Sample answer:
I was asked to create 2 rectangles and 4 triangles using my rectangle.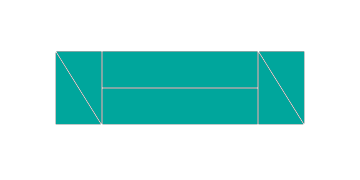
Grades 3–5

Decimal Decorations
What You’ll Need: No materials necessary Ask students what the greatest and least possible answers are for . – . if the digits from 1 to 9 can be used only once. Answer: The greatest possible answer is 97.47 with the equation being 98.7 – 1.23. The least possible answer is 2.43 with the equation being 12.3 – 9.87.
Secret Seeker
What You’ll Need:
No materials necessary
Share these instructions with students:
Play in pairs. Each player secretly writes down a two-digit number and four facts or clues about that number. Player A starts by reading out their first clue. Player B can either guess the number or ask for the next clue. Player A continues to reveal clues until either player B has guessed the number correctly or is unable to guess the number. Player B can now begin revealing their clues to player A.
Players get 1 point if they correctly guess the other player’s number. The goal is to guess the number using as few clues as possible. Students receive 1 additional point for each clue they did not need to use to figure out the number. The student with the most points after 5 rounds wins.
Example: Secret number: 12
Clues:
1. It is a multiple of 4.
2. It is half of a number in the 20s.
3. It is not a square number.
4. It can be made by adding two different prime numbers.

Mathematical Mobiles
What You’ll Need:Mathematical Mobiles printout
Pencils
Ask students to get into pairs. Print out the Mathematical Mobiles and have students cut out the shapes. Then share these instructions with students:
Each player writes a two-digit number at the top of their mobiles. This number must be an even number. Each side of the mobile must be equal to the other and equal the number on the top of the “mobile.”
Players then choose up to four shapes per side and assign each type of shape a number. Players write their numbers on their shapes and place the shapes on their mobile. Players then choose one shape’s number to keep secret and turn all instances of this shape face down on their mobile. They then show the other player their mobile. Both players attempt to figure out what the other’s secret number is. Players that successfully figure out the other player’s secret number earns 1 point. The player with the most points after 3 rounds wins.
Example: Maeve chooses 22 as her two-digit number and writes it at the top of her mobile. She chooses 2 squares and a triangle for the left side and a square, 2 triangles, and a circle for the right side. She chooses 4 for the squares, 3 for the triangle, and 1 for the circle. Maeve decides to keep the triangles’ number a secret and puts the triangles face down. Maeve then hands her mobile to her partner, Jeff, while Jeff hands his mobile to Maeve. Jeff knows that 22 divided by 2 is 11, so each side must equal 11. Jeff looks at the left side and adds the 2 squares together to make 8. This leaves 3 left over. Jeff realizes that the triangle is 3. To check his answer, Jeff tests the right side. He adds the square, 2 triangles, and the circle together. His check comes out to 4 + 3 + 3 + 1 = 11. This means that Jeff’s calculation is correct, and he earns 1 point.

Pattern Puzzles
What You’ll Need:Pattern Puzzles Grids and Clues printout
Students are given a blank 3 × 3 grid and three pattern clues. Students must use these clues to fill in the blank grid. Some clues overlap each other. The grid must contain three squirrels, three cats, and three dogs. For an added challenge, ask students to make their own clues and share them with a partner.
Grades 6–8

Calculator Conundrum
What You’ll Need:
No materials necessary
The 6 key is not working on your calculator.
How can you use the calculator to figure out 69.4 × 6 without using the 6 key?
Sample answer:
I would multiply 70.4 by 3 and then by 2; that would be the same as 70.4 × 6. That is one more 6 than 69.4 × 6, so I would subtract 6. The answer is 416.4.

Two-Thirds Trek
What You’ll Need:
Colossal Calculations
What You’ll Need:
No materials necessary
Use digits from 1 to 9 in the blanks to create an equation that has as great a solution as possible.
x – = x +
Sample answers:
3x – 9 = 2x + 8, so x = 17
5x – 8 = 4x + 9, so x = 17

Mean-Median Mediation
What You’ll Need:
No materials necessary
Create a couple of sets of data where the mode is double the median. Is the mean greater than the median? Explain your answer.
Sample answer:
I think the mean is usually greater than the median when the mode is double the median.
To test this, I used the numbers 1, 3, 5, 10, and 10. The mode is 10 and double the median of 5. The mean is (frac{29}{5}) = 5.8, which is greater than 5.
Then I tried the numbers 1, 2, 4, 8, and 8. The mode is 8 and double the median of 4. The mean is (frac{23}{5}) = 4.6, which is greater than 4.
Since the mode is higher than the median, the numbers higher than the median would count more than the numbers lower than the median when you’re calculating the mean, so the mean would have to be greater than the median.