Digit Drop

What You’ll Need: Digit Drop printout Print and cut out the number cards from the Digit Drop printout. Then give students these instructions: Use a different digit in each blank to make the statement below true. Think of a few possible answers.         +     =         –      Sample answers: 23 + 9 = 40 – 8 73 + 9 = 84 – 2

Route to Ten

What You’ll Need: No materials necessary You add 2 different numbers and then subtract 2 different ones, and you end up with a 10. What numbers could you have used? Sample answers: 8 + 3 – 1 – 0 = 10 12 + 7 – 4 – 5 = 10

Two-Step

What You’ll Need: Two-Step printout Print and cut out the number cards from the Two-Step printout. Shuffle the cards, and place them face down in a pile. Then give students these instructions: Play with a partner or in a small group. Each player picks up 3 cards without revealing them to the other players. Take turns. On your turn, pick up another card. If 1 card in your hand has a number that is exactly 2 more than another, reveal those cards to the other players, and place those cards face up in front of you. Play until there are no more cards to pick up. Players get 1 point for each pair of cards in front of them. The player with the most points wins. Example: Jeffrey picks up a 3, 0, and 9. Rachel picks up a 2, 7, and 9. On Jeffrey’s first turn, he picks up a 4. He doesn’t have any cards that are 2 more than another, so he ends his turn. On Rachel’s first turn, she picks up a 12. She looks at her cards and notices that 9 is 2 more than the 7 in her hand, so she places them face up in front of her. She gets 1 point. Jeffrey starts his second turn. Jeffrey and Rachel play until there are no more cards to pick up.

Clay Creations

What You’ll Need: Different coloured modelling clay Using modelling clay, form numerals in different colours.

Algebraic Agreement

What You’ll Need: No materials necessary Use a different digit for each different letter to make this statement true: ABCD × A = EFDB Sample answer: 3214 × 3 = 9642

Product Plots

What You’ll Need:
Product Plots printout

Using the Product Plots printout, write each digit from 1 to 9 in the squares of each chart so that the products at the end of each row and column make sense.

Sample answers:
Sample answers can be found in the Product Plots printout.

Value Vacancy

What You’ll Need:
No materials necessary

What value makes sense for Q? Explain how you got your answer.
Sample answer:
25
I noticed that in each row, you can multiply the first two numbers and then add the third number to get the fourth number.

Fraction Forming

What You’ll Need:
Fraction Forming printout

Print and cut out the number cards from the Fraction Forming printout. Shuffle the cards, and place them face down in a pile. Then give students these instructions:
Play in pairs or in a small group. Each player picks up two cards without looking at them and places them face down one over the other to form a fraction. The first card they pick up is the numerator, and the second card they pick up is the denominator. Players turn over their cards and determine whose fraction is closest to (frac{1}{2}). The player with the fraction closest to (frac{1}{2}) gets a point. Mix the cards back into the pile of cards for the next round. The first player to get 10 points wins.

Example:
Tina picks up two cards and places them face down in front of her. She then turns them over to reveal that the numerator is a 5 and the denominator is an 8, so her fraction is (frac{5}{8}). She figures out that her fraction is (frac{1}{8}) away from (frac{1}{2}).
Louise picks up two cards and places them face down in front of her. She then turns them over to reveal the numerator is a 3 and the denominator is a 7, so her fraction is (frac{3}{7}). She figures out that her fraction is the same as (frac{6}{14}), which is (frac{1}{14}) away from (frac{1}{2}).
Jacob picks up two cards and places them face down in front of him. He then turns them over to reveal the numerator is a 5 and the denominator is a 3, so his fraction is (frac{5}{3}). He figures out that his fraction is 1(frac{2}{3}), which is more than 1(frac{1}{2}).
Louise gets a point because her number is closest to (frac{1}{2}).

Calendar Calculations

What You’ll Need: No materials necessary The counting numbers below are written with each row two numbers longer than the row above it.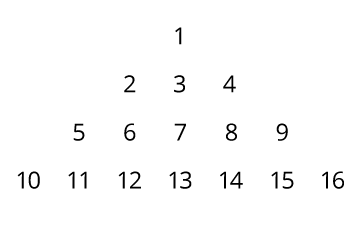 In what row will the number 2022 appear, and how do you know? Answer: I notice that the last number in the first row is 1², the last number in the second row is 2², the last number in the third row is 3², and the last number in the fourth row is 4². I realize that I have to figure out the biggest square number that is less than 2022. I know that √2022 = 44.9. I know that 44², which equals 1936, ends the 44th row. I also know that 45², which equals 2025, ends the 45th row. 2022 is less than 2025, so 2022 is in the 45th row.

Triangle Test

What You’ll Need:
No materials necessary

Sam figured out an interesting way to determine Pythagorean triples, the whole-number side lengths for right triangles. Read through Sam’s theory below.
Choose any odd number. That number will be one side of the triangle. Then square it, and figure out two numbers that are 1 apart that add to the square. Those two numbers are the other two sides of the triangle.
Test Sam’s theory out to see if you agree that it always works.
For example, if you chose 7, you’d look for two numbers that are 1 apart that add to 7² = 49. It would be 24 and 25, so a triangle with side lengths of 7, 24, and 25 is a right triangle. You can check and see that 7² + 24² = 625, which is 25², so it works.

Sample answer:
I think it does.
I tried 5–12–13, 9–40–41, 11–60–61, and 19–180–181, and they all worked.
5² + 12² = 169 = 13²
9² + 40² = 1681 = 41²
11² + 60² = 3721 = 61²
19² + 180² = 32 761 = 181²

Possibility Prediction

What You’ll Need:
Two number cubes

Give students these instructions: Roll two number cubes 20 times. Predict which of the possibilities below is most likely. Test your prediction. A: I will roll at least one 6 six times. B: My rolls will add up to 7 six times. C: I will roll doubles at least once.

Example: Elva predicts that the most likely possibility is rolling at least one 6 six times. Elva experimented by rolling her number cubes 20 times. 1, 1 1, 3 2, 4 2, 6 1, 4 2, 2 1, 5 5, 4 4, 6 5, 5 5, 4 1, 2 5, 4 6, 3 6, 5 1, 4 5, 6 6, 2 1, 3 6, 2 Elva rolled a 6 seven times. Her rolls never added up to 7. She rolled three doubles. Elva’s prediction was correct.

Quadrant Quest

What You’ll Need: Quadrant Quest printout

Give students these instructions: Choose four points on the coordinate grid from the Quadrant Quest printout to make a trapezoid so that two points are 3 apart, two points are 5 apart, and two points are 13 apart. The points must be in different quadrants.

Example: I chose (4, −2) and (4, 1). They are 3 apart. I chose (−9, 1) since it is 13 away from (4, 1). I chose (−1, −2) since it is 5 away from (4, −2). Therefore, the four points are (4, −2), (4, 1), (−9, 1), and (−1, −2).