Shareables
Grades K–2

Block Builder
What You’ll Need: Red pattern blocks What shapes can you make using exactly 6 red pattern blocks? They have to touch to make one whole shape. Sample answer: I made shapes with 14 sides but also a shape with 6 sides.

Square Sequences
What You’ll Need:
A variety of shapes in a variety of colours
Create a pattern where the third shape and the eighth shape are squares.
Sample answer:
I made these patterns:

Ten-Frame Fascination
What You’ll Need:Ten-Frame Fascination printout
Counters
Print and cut out the 10-frames from the Ten-Frame Fascination printout. Provide students with the 10-frames and counters. Then give students these instructions:
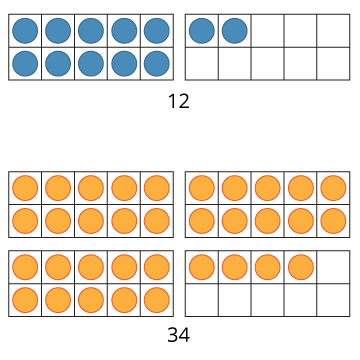
What numbers can you represent where the number of counters in the last unfilled 10-frame is one more than the number of full 10-frames? What do you notice about the numbers?
Sample answer:
I notice that the ones amount is always one more than the tens amount.

High or Low
What You’ll Need:High or Low printout
Print and cut out the number cards from the High or Low printout. Shuffle the cards and place them face down in a pile. Then give students these instructions:
Play with a partner or in a small group. Each player picks up two cards without showing them to the other players. Each player adds their cards together. If the sum of their cards is 4 or 14, they get 2 points. If the sum of their cards is 5 or 15, they get 1 point. The first player with 10 points wins.
Example:
Codey picked 7 and 1. He adds them together to get 8. Codey does not get any points.
Melanie picked up 9 and 6. She adds them together to get 15. Melanie gets 1 point because the sum of her cards is 15.
Henry picked up a 1 and 3. He adds them together to get 4. Henry gets 2 points because his numbers equal 4.
Grades 3–5

Consecutive Count
What You’ll Need: No materials necessary What numbers are you able to write as the sum of consecutive numbers (i.e., numbers that are “in a row” numbers). You can use any number of consecutive numbers. Are there any numbers you cannot write that way? Answer: 1 = 0 + 1 2 cannot be written that way. 3 = 1 + 2 4 cannot be written that way. 5 = 2 + 3 6 = 1 + 2 + 3 7 = 3 + 4 8 cannot be written that way. 9 = 4 + 5 10 = 1 + 2 + 3 + 4 I can see that any odd number works, but only some even numbers do.
Square Seventeen
What You’ll Need: No materials necessary Square numbers are numbers such as 3 × 3 or 8 × 8, where the two numbers multiplied are the same. How can you arrange the numbers from 1 to 17 in a row so that each pair of numbers next to each other adds to a square number? Sample answer: 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17
First to Five
What You’ll Need:
Grid Guide
What You’ll Need:Grid Guides printout
Print and cut out the grid from the Grid Guide printout. Then give students these instructions:
Colour two squares on your grid. Create a set of exactly five instructions, including instructions about moving up or down a certain number of spaces, left or right a certain number of spaces, or quarter or half turns either clockwise or counterclockwise that will get you from one of the coloured squares to the other.
Sample answer:
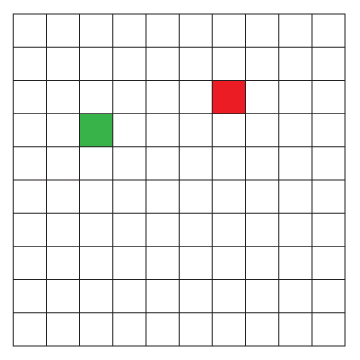
Go up 1 space.
Go right 3 spaces.
Go down 1 space.
Go right 1 space.
Go up 1 space.
Grades 6–8

Tearing Triangles printout
What You’ll Need:Tearing Triangles printout
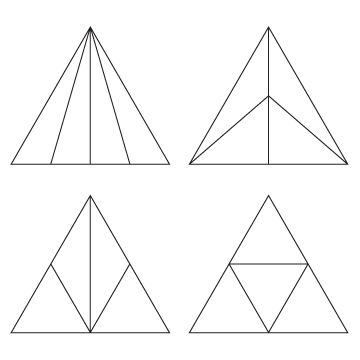
What are some different ways to cut an equilateral triangle into four triangles of equal area?
Sample answer:

Statistic Seekers
What You’ll Need:
Concentration: Fractions and Percents II
What You’ll Need:
Team-Up Timing
What You’ll Need:
No materials necessary
Connor can finish a job in 10 hours, but it would take Noah 8 hours.
How long would it take them if they worked together?
Sample answer:
I figured out that in 1 hour, Connor does (frac{1}{10}) of the job and Noah does (frac{1}{8}) of the job. This means that in one hour, Connor and Noah complete (frac{1}{10}) + (frac{1}{8}) of the job. That is (frac{9}{40}) of the job. That means that in 4 hours, they would do (frac{36}{40}) of the job, or (frac{9}{10}) of the job.
For the other tenth, it would take (frac{1}{9}) of 4 hours. Since 4 hours is 240 minutes, then (frac{1}{9}) of that time is 26(frac{2}{3}) minutes, so the total amount of time is a little less than 4(frac{1}{2}) hours, about 3(frac{1}{3}) minutes less.