Greatest Guess

What You’ll Need: Number cards (1–10) Print and cut out the number cards. Shuffle and place the cards face down in a pile. Then give students these instructions: Play in pairs. Each player picks up two cards without looking at them. Players hold their cards, one in each hand, without revealing their cards to the other player. The first player guesses which of the other player’s two cards is greater and points to it. The second player reveals the numbers on their two cards. If the first player correctly guesses the card with the greater number, they get a point. If the numbers on the cards are equal, they do not get a point. The second player then takes a turn guessing which of the first player’s cards is greater. The first player to get to 10 points wins. Example: Dana and Warren each pick up two cards without looking at them. Dana guesses first. She guesses that the card in Warren’s left hand is going to have a greater number than the card in his right hand. Warren reveals both cards, showing a 6 in his left hand and a 7 in his right hand. Dana does not get a point because she did not guess the card with the greater number. Warren guesses that the card in Dana’s right hand is going to have a greater number than the card in her left hand. Dana reveals both cards, showing a 2 in her left hand and an 8 in her right hand. Warren gets a point because he guessed the card with the greater number.

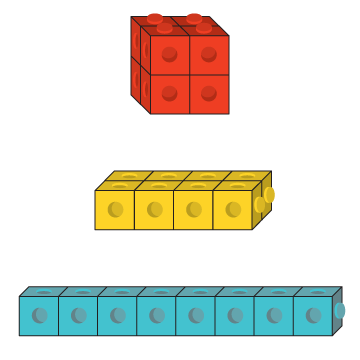
Cube Construction

What You’ll Need:
8 linking cubes

How many different structures can you build with 8 linking cubes?

Sample answer:
I made these structures:

10-Frame Total

What You’ll Need: Counters 10-Frame Total printout

Play in pairs. Each player picks a number less than 10 and places that number of counters on one of the 10‑frames from the 10‑Frame Total printout. Each player takes a turn spinning the spinner from the 10‑Frame Total printout and placing that number of counters on their 10‑frame. Players get 2 points if there are exactly 10 counters on their 10‑frame. Players get 1 point if they fill a frame but have extra counters left over. Players get 0 points if there are fewer than 10 counters on their 10‑frame. The first player to 10 points wins.

Example: Geordie decides to place 3 counters on his 10-frame. He spins the spinner and gets a 7. He places 7 counters on his 10‑frame. Geordie gets 2 points because he has 10 counters on his 10‑frame. Tasha decides to place 4 counters on her 10‑frame. She spins the spinner and gets an 8. She places 8 counters on her 10‑frame, with 2 extra counters remaining. Tasha gets 1 point because she has extra counters after filling her 10‑frame.

Toothpick Predictions

What You’ll Need: 10 toothpicks Choose objects from your house or classroom that you predict will be 10 toothpicks long. Check your predictions. Sample answer: I predicted that my microwave would be 10 toothpicks long. When I checked my prediction, my microwave was a little less than 9 toothpicks long.

Pattern Picker

What You’ll Need: Pencil and paper Create a pattern where you choose the first two numbers in the pattern and continue the pattern by adding the previous two numbers to get the next one. Your pattern must include the numbers 58 and 152, and 58 and 152 cannot be the first two numbers. Answer: 2, 6, 8, 14, 22, 36, 58, 94, 152, 246, 398, …

Digit Decisions

What You’ll Need: Number cards (1–9) Cut out and shuffle the number cards. Place the cards face down in a pile. Then give students these instructions: Play in pairs or in a small group. Each player picks up four number cards to create a three-digit number and a one-digit number. Students can choose to either divide the three-digit number by the one-digit number or multiply the two numbers. The number of points they get is the tens digit in their quotient or product. After each round, players return their cards to the pile and reshuffle the cards. The first player to 30 points wins. Example: Perry picks up the numbers 4, 1, 4, and 5. He multiplies 415 × 4. His product is 1660. Perry gets 6 points because the tens digit is a 6. Amara picks up the numbers 7, 2, 9, and 5. She divides 957 ÷ 2. Her quotient is 478.5. Amara gets 7 points because 7 is in the tens digit place.

Fraction Foraging

What You’ll Need: No materials necessary A fraction close to 1 and a fraction close to (frac{2}{5}) have numerators and denominators that are 20 apart. What could they be? Example: (frac{90}{110}) and (frac{15}{35})

Face Facts

What You’ll Need: Two triangular prisms (or the material to make them) Provide students with two plastic or wooden triangular prisms, or allow students to create their own using modelling clay. The triangular faces should be congruent. Then provide students with these instructions: Put together two faces to make a larger object. How many faces does that object have? How do you know? Example: I stacked the triangular faces together and made a longer triangular prism with 5 faces. I also put two rectangles together and made a prism with 6 faces. If I fit two faces together but not perfectly, I could end up with even more faces.

What Else Do You Know?

What You’ll Need:
No materials necessary

Present an “If you know ______, what else do you know?” activity that revolves around percent. Use the sample questions below.

If you know that

• 15% of a number is 20, what else do you know?
• 30% of a number is 40, what else do you know?
• 30% of one number is the same as 20% of another number, what else do you know?

Sample answers:

• If you know that 15% of a number is 20, then 30% of that number is 40, 45% is 60, 90% is 120, 5% is 6(frac{2}{3}), and the number is more than 100 but not a lot more.
• If you know that 30% of a number is 40, then you know that 15% of that number is 20, 45% of that number is 60, 60% of that number is 80, 90% of that number is 120, 5% of that number is 6(frac{2}{3}), and the number is more than 100 but not a lot more.
• If 30% of one number is the same as 20% of another, the second number is 1.5 times the first. I also know that 30% of the second number is 1.5 times 20% of the second number, and 20% of the first number is (frac{2}{3}) of 30% of the first number.
  

Square Root Riddles

What You’ll Need:
No materials necessary

Solve these problems:

• The square root of a number is about 40 less than the number. What could the number be?
• The square root of a number is about 3500 less than the number. What could the number be?
• The square root of a number is about 1 000 000 less than the number. What could the number be?
• The square root of a number is greater than the number. What could the number be?
  

Sample answer:

• 47
• 3560
• 1 001 001
• (frac{1}{4})
  

Combination Conundrum

What You’ll Need: No materials necessary What is the greatest whole number you cannot write as a combination of 4s, 7s, or 4s and 7s? Explain how you got your answer. Answer: 17 There is no way to combine 4s and 7s to make 17, but 18, 19, 20, and 21 are all possible combinations. 18 = 7 + 7 + 4 19 = 7 + 4 + 4 + 4 20 = 4 + 4 + 4 + 4 + 4 21 = 7 + 7 + 7 Since you can make 18, 19, 20, and 21 using 4s and 7s, you could just add a 4 to each of them to get 22, 23, 24, and 25. Then you could add 4 to each of these and write 26, 27, 28, and 29. You just keep adding 4 to the last group of 4 and you end up writing all the numbers.

Prism Potential

What You’ll Need:
Calculator (optional)

Pose this problem for students: You start with a rectangular-based prism and calculate the surface area. Which of these calculations would make the surface area increase by more: adding 5 to one of the sides of the base or adding 5 to the height? Show your thinking.

Sample answer:
I started with a rectangular-based prism with a base width of 4, a base length of 8, and a height of 10. I made all the numbers different to make the changes in surface area more obvious. The original prism has a surface area of 2 × (4 × 8 + 4 × 10 + 8 × 10) square units, or 304 square units. I decided to start with the width of the base. I changed the 4 to 9, and the surface area changed to 2 × (9 × 8 + 9 × 10 + 8 × 10) square units, or 484 square units. Then I changed the length of the base from 8 to 13, and the surface area changed to 2 × (4 × 13 + 4 × 10 + 13 × 10) square units, or 444 square units. Then I changed the height from 10 to 15, and the surface area changed to 2 × (4 × 8 + 4 × 15 + 8 × 15) square units, or 424 square units. I think changing the smallest dimension would increase the surface area by the greatest amount. In this case, adding 5 to one of the sides of the base increased the surface area by more.