Ask Marian

Sometimes people think that a misleading graph is a graph with a mistake in it, but that’s not what it is. A misleading graph is a graph that gives you an inaccurate impression of the data.

For example, if one company had a 20% share of the market, another had a 22% share, and a third company had 19%, the differences do not seem very big. But take a look at this graph that the company with the 22% share might use.

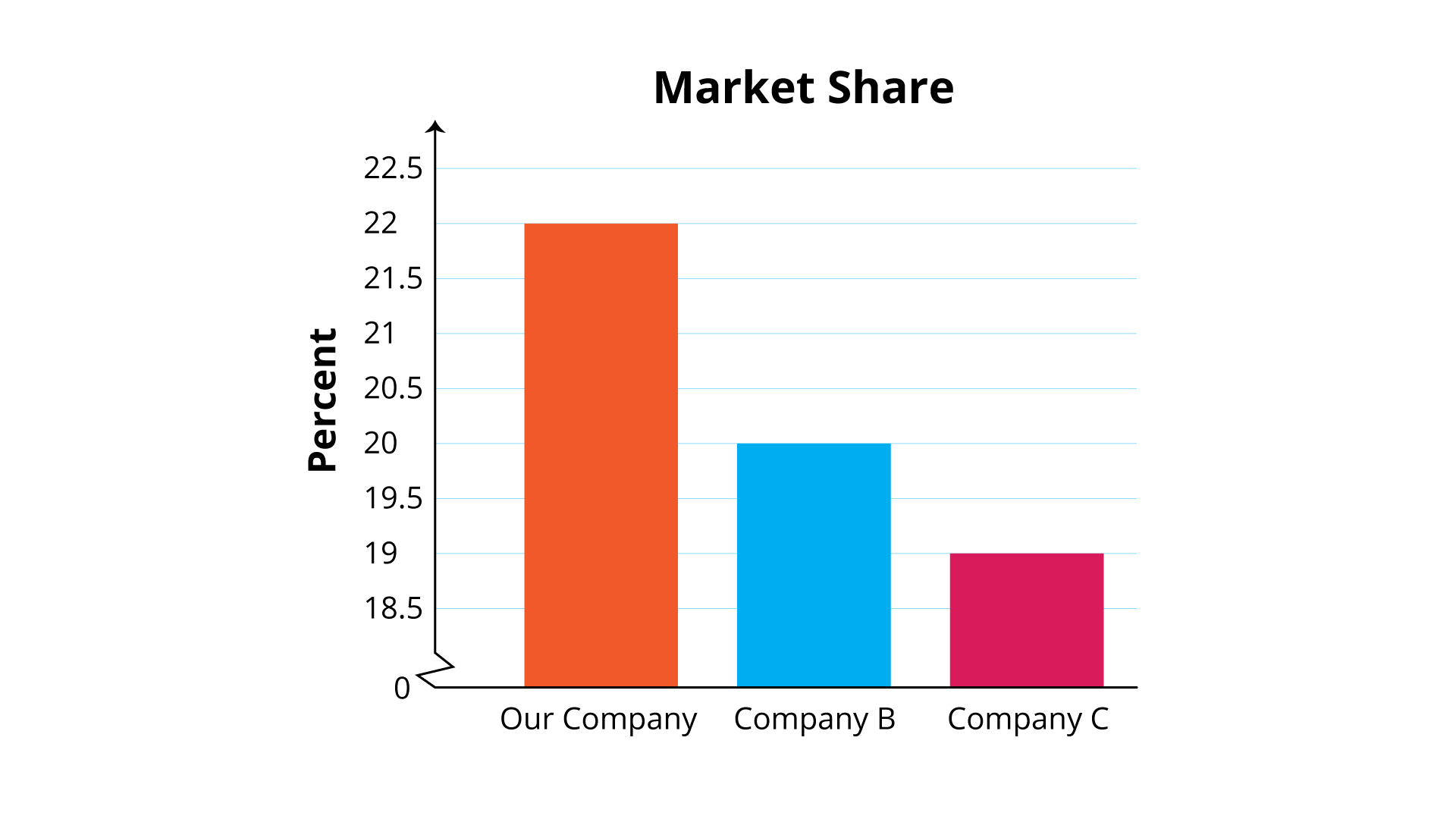
By not starting the y-axis at 0 and choosing this scale, the differences seem much greater than they really are.

Other ways that graphs might be misleading include the following:

• using picture icons in the graph but making something that should look twice as big look four times as big by making it both wider and taller
• reversing the scale on an axis to make something that should look like a decrease look like an increase instead

Sometimes these approaches are deliberate to convey an impression that may not be accurate. However, sometimes a misleading graph is just the accidental result of someone who is not being thoughtful about how to create the graph properly.

Often we think that the rules for the order of operations are arbitrary, but they actually are not. There are reasons that the order is what it is. Here is a little bit of insight into why.

Suppose you have the expression 4 + 5 × 3. The rules tell us to do the multiplication first, and this is why: 5 × 3 means 3 + 3 + 3 + 3 + 3, so 4 + 5 × 3 means 4 + 3 + 3 + 3 + 3 + 3. Clearly, it makes no sense to add 4 and 5 first and then multiply by 3. That would not follow what the expression means.

Here’s another example: 3 × (5 + 7). We are supposed to do what is in the brackets or parentheses first. This is because 5 + 7 is something you want to add 3 times, so the same expression is 5 + 7 + 5 + 7 + 5 + 7. Clearly, it is 3 groups of 12, not 3 × 5 + 7, which would not be enough.

Here’s one more example: 3 + 5². We are supposed to do the exponent first, and that’s because it’s a multiplication. As shown above, it makes sense to do multiplication before addition.

This is just a start into why all the rules for the order of operations are what they are.

Many students think of themselves as either good at math or bad at math, and those self-evaluations can sometimes get in the way of student success. For example, if students see themselves as good at math and encounter a difficult problem that causes them to struggle, they might just believe there is something inappropriate about the problem and not continue to try to solve it; they might think that if they didn’t get the answer right away, it’s a bad question. On the other end, students who see themselves as bad at math might not even try, even when they might be successful.

Part of our teaching needs to focus on helping students develop positive math identities. We need to instill the beliefs that students are capable of being successful in math when they work at it and that they shouldn’t see everything as only one thing or only another. Even people who are often successful can, and perhaps should, encounter more puzzling situations.