Counter Clues

What You’ll Need:
No materials are necessary, but you can provide counters (red, green, and blue) if you wish.

Tell students you have a riddle for them:
There is 1 more red counter than there are blue counters. There are 2 fewer green counters than red counters. If I tell you how many green counters there are, can you tell me how many red and blue counters there are?

Sample answers: If there were 5 green counters, there would be 7 red counters and 6 blue counters. OR If there were 8 red counters, there would be 7 blue counters and 6 green counters. OR If there were 4 blue counters, there would be 5 red counters and 3 green counters.

Challenge students to come up with their own version of this riddle. They can choose which colour counter to tell about. They could then get in small groups and let the other members of their group try to figure out the other numbers.

Difference Deduction

What You’ll Need:
Number cards (0–20)

Print and cut out the number cards. Shuffle the cards, and place them face down in a pile. Then give students these instructions: Play in pairs or in a small group. Each player picks up two cards. Each player subtracts their smaller number from their larger number and calculates the difference. If the difference is more than the smaller number, you get 1 point. The first to get 10 points wins.

Example: Tina picked up an 18 and a 10. 18 – 10 = 8. 8 is less than 10, so Tina does not get a point. Kieran picked up an 11 and a 4. 11 – 4 = 7. 7 is more than 4, so Kieran gets a point.

Memory Missions

What You’ll Need:
5 or 6 objects
Paper and pencil

Use these and similar visual memory tasks over time:
Show students 5 or 6 objects arranged randomly. Students look for a short time and then close their eyes. Move 1 object. Students open their eyes and have to say which object was moved.
Show students 5 or 6 objects arranged randomly. Students look for a short time and then close their eyes. Switch the position of 2 objects. Students open their eyes and have to say which objects were switched.
Show students 5 objects arranged randomly. Students look for a short time and then close their eyes. Replace 1 object with something different from all the other objects. Students open their eyes and have to say which object was replaced.
Show students an irregular shape or design made of 5 or 6 lines. Students look for a short time. Hide the original shape. Students try to recreate what they saw.

Up and Down

What You’ll Need:
Deck of number cards (1–10)

Shuffle the deck of number cards provided. Two students can play against each other. Each student starts with five cards. Put the rest of the cards face down in a pile. Start the game by flipping over a card from the pile. Have students take turns putting down a card from their hand that is either one more or one less than the starting number (e.g., if the first card that was flipped over was 5, a player could put down a 4 or a 6). If a player cannot put down any card from their hand, they should draw a new card from the face-down pile and add this card to their hand; this ends their turn. The first player to get rid of all their cards wins.

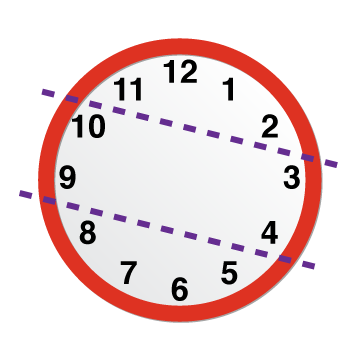
Cut-Up Clock

What You’ll Need:
Paper and pencil

Draw and label a clock without hands. Draw two lines to divide the face of the clock into three sections. The numbers in each section add up to the same total as each of the other two sections. What numbers are in each section?

Answer:
The top section includes 11, 12, 1, and 2.
The middle section includes 9, 10, 3, and 4.
The bottom section includes 7, 8, 5, and 6.
The sum of each section equals 26.

Magic Square

What You’ll Need:
Magic Square printout
Pencil

Print out the Magic Square printout. A magic square is a square divided into an equal number of rows and columns, in this case 3 rows and 3 columns. All rows, columns, and diagonals should add to the same amount.
For an added challenge, create your own magic square and share it with a classmate.

Answer:
Top row: 7, 17, 15
Middle row: 21, 13, 5
Bottom row: 11, 9, 19

Remainder Reveal

What You’ll Need: Number roller (0–9) Play with a partner. On your turn, roll the number roller four times to get numbers to fill in the spaces in ☐☐☐ ÷ ☐. Players can choose where each number is placed within the blanks. If you roll a 0, reroll for a new number. The number of points you get is the remainder when you divide. The first player to reach 20 points wins. Example: Taha rolls a 3, 6, 1, and 0. He rerolls to replace the 0 and gets a 2. Using his numbers, he makes the expression 213 ÷ 6, which equals 35 with a remainder of 3. Taha gets 3 points because his remainder is 3. Sabrina rolls a 7, 9, 7, and 3. Using her numbers, she makes the expression 737 ÷ 9, which equals about 81 with a remainder of 8. Sabrina gets 8 points because her remainder is 8.

Sign Strings

What You’ll Need: Paper and pencil Write down the digits 9, 8, 7, 6, 5, 4, 3, 2, and 1 in sequence. Place operation signs between the digits so that the digits make a total of 99. You can keep the digits together to make numbers that are greater than one-digit numbers. Sample answers: 9 + 8 + 7 + 6 + 5 + 43 + 21 OR 9 + 8 + 7 + 65 + 4 + 3 + 2 + 1 OR 98 + 7 – 6 – 5 + 4 + 3 – 2 × 1

Triangle Trouble

What You’ll Need:
No materials necessary

What fraction of the rectangle is shaded?

Now make another rectangle where the shaded part, made up of triangles, is (frac{2}{3}) of the area.

Answer:
The original rectangle has an area of 3bh where b is the base of each triangle and h is the height. Together, the three triangles have an area of 3bh ÷ 2. So, the triangles are (frac{1}{2}) the area.
For my new rectangle, I thought about a rectangle with base b and height h. I realized that if I could split it into 6 triangles of the same size, even though I had to split one of the triangles into two half-triangles. Then I chose 4 of the triangles, which would be (frac{2}{3}) of 6 triangles. equal sections and 4 of them were made up of identical triangles, then (frac{2}{3}) of the rectangle would be made up of the triangles.
So, it could look like this:

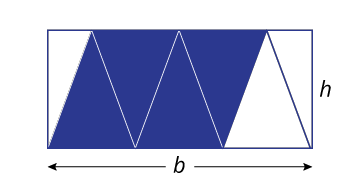
The triangle height is h and the base of each triangle is (frac{b}{3}).
So, the area of all four triangles is 4 x (frac{bh}{3}) ÷ 2 = (frac{2bh}{3}).

Mean-Median Integers

What You’ll Need:
Mean-Median Integers printout

Print and cut out the integer cards from the Mean-Median Integers printout. Shuffle the integer cards, and place them face down in a pile. Then give students these instructions:
Play with a partner or in a small group. Each player picks up five cards and determines the median and mean of their cards. Players get no points if their median is more than their mean. Players get 1 point if their median is less than their mean. Players get 2 points if their mean and median are the same. The first player to get to 10 points wins.

Example:
Pamela picked up the integers –2, 0, 5, 2, and –5. The median is 0 and the mean is 0, so she gets 2 points.
William picked up the integers 5, 1, –4, 5, and 0. The median is 1 and the mean is 1.4, so he gets 1 point.

Quotient Conundrum

What You’ll Need:
Deck of digit cards (0–9)

Share this game that students can play with one another in class:
Shuffle a set of digit cards. Each player draws five cards and chooses three of these to make a three-digit number. Players then choose one of their remaining cards as the number to divide their three-digit number by. Both players should have a division sentence in this format: Any 3 cards ÷ 1 card = quotient. The player with a quotient closest to 100 scores 1 point. If both players are equally close, each player scores 1 point. The player with the most points after 5 rounds wins.

Picking Percents

What You’ll Need:
Pencil and paper

Create interesting figures where 15%, 40%, and 20% are each used once in the following blanks:
The head height is ____% of the height of the whole body.
The distance from the waist to the feet is ____% of the height of the whole body.
The arm length is _____% of the length of the leg.
Rearrange the numbers and create a new figure, and then do it again. Which of your three figures seems best?

Sample answer:
I think the figure I made below makes the most sense.
The head height is 15% of the height of the whole body.
The distance from the waist to the feet is 40% of the height of the whole body.
The arm length is 20% of the length of the leg.