Fill in the Grid

What You’ll Need:
Fill in the Grid printout

Print and cut out the grid and rectangles from the Fill in the Grid printout. Then share these instructions with students:
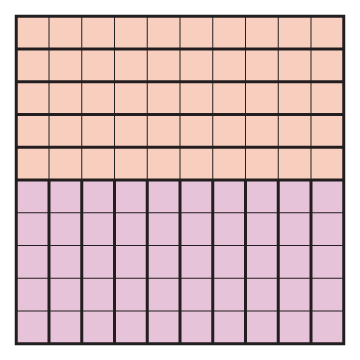
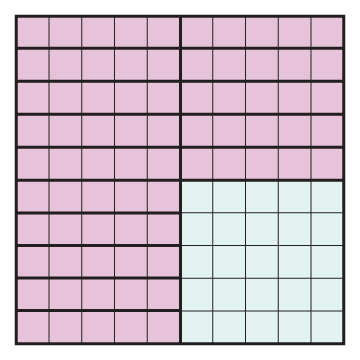
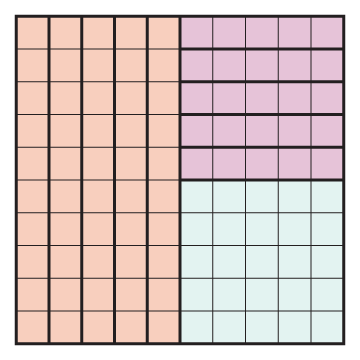
Find as many ways as you can to show 100 by filling the 10 × 10 grid with the rectangles you have.

Sample answer:
Here are some of the ways I showed 100 on the 10 × 10 grid:

Tile Task

What You’ll Need: 8 square tiles Provide each student with 8 square tiles. Have them make different shapes using all their tiles. Encourage students to create shapes with different numbers of sides. Ask them how many sides each of their shapes has. Sample answer: Here are two shapes that I created. My first shape has 4 sides. My second shape has 10 sides.

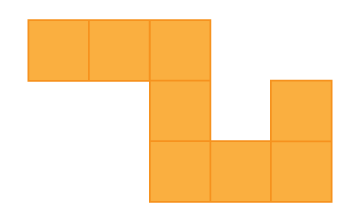
How Much More?

What You’ll Need: Number cards (1–10) 16 counters

Cut out and shuffle the number cards. Place the cards face down in a pile. Then share these instructions with students:

Play with a partner. In each round, each player draws a card from the deck. Players then show each other their cards. If a player’s card shows a number that is 1 or 2 more than the other player’s number, that player gets 1 counter. If a player’s card shows a number that is 3 or more than the other player’s number, that player gets 2 counters. If the cards have the same value, neither player gets a counter. The first player to get 8 counters wins.

Example: Priya and Tasha each pick up a card. Priya picks up a 5. Tasha picks up a 2. They show each other their cards. Priya’s number is 3 more than Tasha’s number. Priya gets 2 counters. They each pick up a new card. Priya picks up a 2. Tasha picks up a 4. They show each other their cards. Tasha’s number is 2 more than Priya’s number. Tasha gets 1 counter.

Number Rod Writing

What You’ll Need:
Number Rod Writing printout

Cut out the rods on the Number Rod Writing printout, and give these instructions to students: Use the rods to form letters. Each rod has a number value written on it. With your letters, make a word that is worth close to 70.

My Mathematician

What You’ll Need:
Paper and pencil

Ask students to draw a picture of what they think a mathematician looks like. Ask them why they chose to draw the mathematician that way. Encourage students to talk about biases.

Sample answers
I drew these mathematicians:

Cereal Study

What You’ll Need: No materials necessary Ask students to come up with a way to estimate how many pieces of cereal might be in a cereal box. Have them justify their method. Sample answer: I could fill a cup with cereal and count how many pieces were in the cup. I could then empty the box into cups and count how many cups were filled. If I counted 250 pieces of cereal in a cup and filled about 11 cups with all the cereal, that would be about 2750 pieces of cereal.

Multiplication Makers

What You’ll Need: Paper and pencil Have students create a game that is helpful for practising multiplication. If students want to test out their game, provide them with the necessary materials. Sample answer: My game is a two-player card game using number cards (1–10). Each player picks up two number cards and multiplies their numbers. The player with the bigger answer gets a point. If players get the same answer, neither of them get a point. The first player with 20 points wins the game. For example, if Jeremy picks up a 2 and 6, his answer is 12. If Suri picks up a 4 and 5, her answer is 20. Suri’s answer is bigger, so she gets the point.

Probable Probability

What You’ll Need: Number cube (1–6) Counters (3 colours) Paper bag Paper Pencil or pen Play with a partner or in a small group. Have one player roll a number cube three times to determine the number of counters of each colour to place in the paper bag. Place the counters in the bag, and shake the bag. A player draws a counter from the bag. They place the counter back in the bag and draw another counter. Repeat for each player, and record their combination in the order it was drawn. Each player predicts if their counter combination will be drawn most often. The players then run an experiment. During the experiment, a player draws a counter from the bag, puts it back, takes another counter, and puts it back. Then the player shakes the bag. The player repeats this 20 times and records the results each time. Players score 1 point if their prediction is correct after 20 draws. Start a new round by drawing new counter combinations for each player. Take turns drawing counters for each round. The player with the most points after three rounds wins.

Example:
Lucan rolls the number cube three times. His results are 3, 2, and 4. He places 3 yellow counters, 2 blue counters, and 4 green counters in a paper bag and shakes the bag. Lucan draws 1 green counter, puts it back into the bag, and then draws a yellow counter. Fizza draws 1 green counter, puts it back into the bag, and then draws another green counter. Since there are more green counters than yellow or blue counters, Lucan and Fizza both predict that Fizza’s combination will be drawn most often. Fizza conducts the experiment. She draws from the bag 20 times and writes down the results. Fizza draws a green counter followed by a green counter 5 times. She draws a green counter followed by a yellow counter 3 times. Fizza’s other 12 draws did not fit either of their counter combinations. Fizza and Lucan each score 1 point since their predictions were correct. Fizza and Lucan start the next round by each drawing new counter combinations.  

Out of Sorts

What You’ll Need:
No materials necessary

Have students think of as many different ways as they can to sort the equations and expressions below.
2x + 3y
3x – 5
y = 3x + 10
p = 2i + 2w
a = (frac{1}{2})bh
3x + 4 = 10
6x + 5y
5x – 8
y = 3x – 7
4x – y
4x – 7
2x – 6 = 10

Sample answers:
I can sort them by whether they are an expression or an equation.
OR I can sort them by whether there is an x in the equation or expression.
OR I can sort them by whether there is more than one letter in the expression or equation.

Helpful Heights

What You’ll Need:
Helpful Heights printout

Share the image on the Helpful Heights printout. Suppose Marcus is 5 ft tall. Ask students how tall they think the tree and the dog might be. Ask them to justify their answer.

Sample answer:
The dog looks about a third of the height of Marcus. This would make the dog about 2 ft tall. The tree looks like it is about 6 times as tall as Marcus. This would make the tree about 30 ft tall.

Integer Inventors

What You’ll Need:
Pencil and paper
Integer Inventors printout

Have students create a game that is helpful for practising the multiplication of integers. If students want to test out their game, provide them with the necessary materials.

Sample answer:
My game is a board game.
You roll a number cube to decide how many spaces to move. Each space either tells you how many spaces to move forward or gives you an integer multiplication question to answer. If you land on a move-forward space, move the number of spaces specified and answer the integer multiplication question. If you land on a question space and get the right answer, stay on that space and your turn ends. If you get the wrong answer, move back 3 spaces from that space and your turn ends. The first person to land on the finish space wins.
A sample of the example game can be found in the Integer Inventors printout.

Multiple Mark-Off

What You’ll Need: 2 number cubes Paper and pencils Play in pairs or small groups. Each player writes the numbers 2 to 9 on a sheet of paper. Players take turns rolling two number cubes and using the numbers they rolled, in either order, to create a two-digit number. If a number on that player’s list is a factor of the two-digit number, they can cross the number off their list. If the player cannot cross off a number, they can roll again for a new two-digit number, but they can do so only once per turn. A player can cross off only one number each turn. The first player to cross off all their numbers wins.

Example:
Elijah rolls two number cubes. His results are 2 and 3. He decides to use 32 instead of 23 because 32 is a multiple of more numbers. Since 23 is a prime number, it’s a multiple of only 1 and 23. 4 × 8 = 32, so he can cross off either 4 or 8. Elijah decides to cross off 8.