As students advance in grade levels, they learn different strategies for adding, subtracting, multiplying, and dividing numbers. Some of these strategies are algorithms. An algorithm is a procedure with all the steps clearly defined. It does not have to be a computation, although we often associate algorithms with computations.

Students learn procedures that are often referred to as standard or conventional algorithms. For example, this procedure below is a conventional algorithm for multiplying 2 two-digit numbers.

But there are alternative algorithms as well. Some students may find these alternatives easier to understand or use. For example, if we multiplied the same numbers in four parts, it would also be an algorithm. It’s often called a partial product algorithm.

Another example of a conventional algorithm is the one for long division below:

Students learn to divide parts of the number, from left to right, determine the closest multiple, subtract, bring down the next digit, and repeat. However, again, there are alternative algorithms that students may find helpful. For example, students might use the partial quotients algorithm.

Students look at the dividend and consider what multiple would be closest. They do this by estimating, usually by multiplying the divisor by 10 or by another easy number. After they figure out what the closest multiple is, students determine the difference between the dividend and the multiple and then consider the closest multiple again. At the end, the partial quotients are added together to make the quotient.

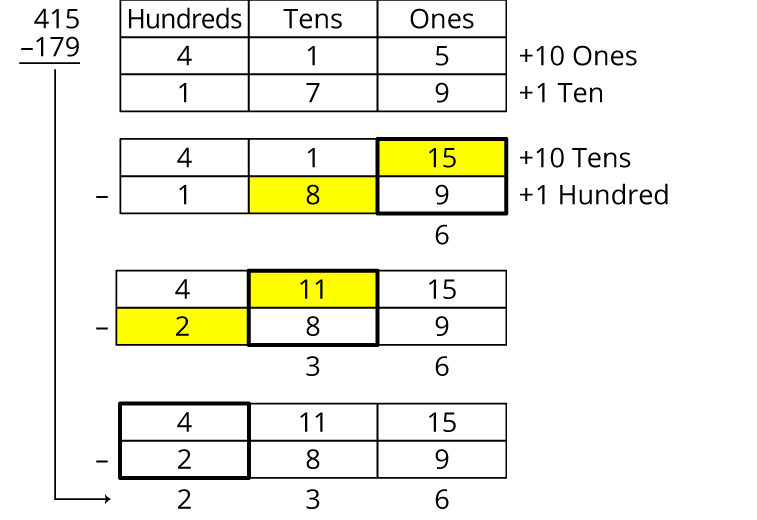
It is important to note that what may be considered a conventional algorithm here in Canada may not be in other countries. For example, in some jurisdictions, students use a different algorithm for subtraction.

In this question, rather than renaming 415 as 4 hundreds, 0 tens, and 15 ones, students add 10 ones to 415 and 1 ten to 179 and then subtract the ones. They repeat this with the tens and hundreds (adding 10 tens to the 415 and 1 hundred to the 179 before subtracting the tens and hundreds) to get the final answer.

So, while some algorithms have traditionally been taught as the standard or convention for many years and are valid methods for students to learn, they should not be the only algorithms. Exposing students to multiple algorithms can show them that there are many different ways of solving the same problem and can encourage them to be flexible in their thinking.