Ask Marian

In this scenario, one of the things we can do is decide what it is about the areas of rectangles, besides how to calculate them, you want students to notice. For example, perhaps there are some relationships you want them to notice or think about.

Here’s one idea: Since the area is the product of the length and width, if the length and width are whole numbers, the area can only be an odd number if both the length and width are odd numbers. So, you could ask students this: Suppose you know the area of a rectangle is an odd number and the side lengths are whole numbers. What else do you know about the rectangle?

A different idea might be that sometimes the number of units in the perimeter is smaller than the number of square units in the area (e.g., 5 × 5), sometimes the number is the same (e.g., 6 × 3), and sometimes it’s more (e.g., 59 × 1). So, you could ask this: Which is usually greater: the number of units in the perimeter of a rectangle or the number of square units in the area?

This gives students a chance to still do lots of area calculations but learn more too.

I believe that speed should never be a requirement of a student’s work. Indeed, there are still teachers who use timed tests, but there are an increasing number of teachers at the higher grades who have come to the realization that being fast is not the be-all and end-all.

This is likely to happen if students think about (frac{4}{5}) ÷ (frac{3}{5}) as how many (frac{3}{5})s fit in (frac{4}{5}), which is actually a good thing.

What they see is this:

So, it seems like (frac{3}{5}) fits in (frac{4}{5}) one whole time, and then there is another (frac{1}{5}) left. So, students think of the answer as 1(frac{1}{5}). But they need to realize that the remaining (frac{1}{5}) is only (frac{1}{3}) of the next (frac{3}{5}) that they would be trying to fit in.

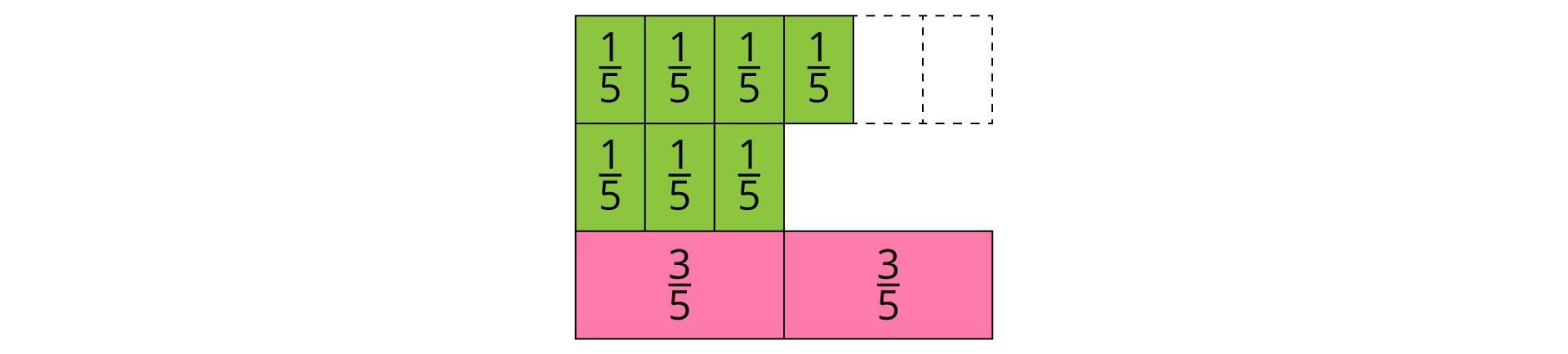
So, if you are counting how many groups of (frac{3}{5})s fit in, it is 1 whole group and one-third of the next (frac{3}{5}), or 1(frac{1}{3}).